Knots

If knots ends are leading to infinity – like in Rope knot theory (Fig 1-2) – open curve  – they are known as knotoids, while typical knots in knot theory have tied-glued-knotted ends (Fig 2-3) – closed curve.

Fig. 1-2: Overhand knot and Figure-eight k. and 3-4: Trefoil and Quatrefoil are from the point of knot theory actually same knots: overhand  resp. F8 knot usually mean open, while tre/quatrefoil knot is usually closed. 

I. Knots list

Knots | Visions in Math (wlu.edu)

3^1 Trefoil 

Trefoil (mathcurve.com)

– trefoil is from Latin – three leaves. One can also treat foil knots as small special knot class..
– is simplest and smallest knot (after unknot))- 
– it is basically overhand knot (w/ glued ends).

– 3:4 Lissajous merged (not doubled) curve (redline pic bellow) in cycle starting state is loosely related to 3^1 knot as quartic curve. Loosely, cause in math terms knots are closed curves, so 3:4 LC are not trefoil knots..

The torus knot T(n, n–1) is equivalent to the n-leaved trefoil knot.

Parametric eq.: 
         x = sint + 2sin2t
          y = cost – 2cos2t
          z = −sin3t  

 

Resp.:  x = cost + 2cos2t
          y = cost – 2sin2t
          z = 2esin3t  
e = 1 – lefthanded
       -1 – RH.

                Quartic curve.

       Lefthanded knt.

      Righhanded knt.

– T(3, 2) torus knot – Torus eq.: 
         x = (4 + cos3t) cos2t
          y = (4 + cos3t) sin2t
          z = esin3t  

 

T(3, 2)

T(2, 3) – parametric equation.

T(2, 3)

– also special case of n = 3/2 Hypotrochoid – see  Conical roses (sigsaly.xf.cz).

W/ q = 3 and w2/ w1 = 2.

– also special case of n = 2/3 Epitrochoid – see  Conical roses (sigsaly.xf.cz)
– as seen above – it is T(2, 3) torus shape, which is often recognized as 4^1 knot, but it is probably more different case of 3^1.

 

W/ q = 2 and w2/ w1 = 3.

– close to special case of n = 1/2 Conical rose – see  Conical roses (sigsaly.xf.cz)
– this is also Durer folium

 

– Mobius strip. w/ 3 half-twist: 
  

 

– Trefoil is chiral knot (see chpt. bellow) – mirrored img. is not equivalent.

– Knot group is isomorphic to braid group.
(x, z | x^2 = y^3) / (a, b | aba = bab)

            Trefoil knotting

3^1≠3^1  Square knot  

– SK is a composite knot – sum of trefoil w/ its reflection (Lpic).
– since it is sqr. knt., it is also ribbon knot (L2down-pic) slice knot.

– achiral and Lissajous knot (Lpic) – nx-z-y-z = (3, 5, 7)
     – Phase rate = (0,7, 1,0)

 3^1≠3^1  Granny knot

– similarly like Square knot it is composite of two identical Trefoil knot (so the second one is not reflected like in SA).
– GK is (unlike SA) not ribbon knot, or slice knot.

4^1  Figure-eight knot 

– Figure-eight knot (mathematics) – Wikipedia 

-F8k also known as listing´s knot  or quatrefoil – second smallest knot after trefoil (+ resp. unknot).
– torus knot T(2, 3), hyperbolic  – see their list in Rpic (endless knot is 7^4 knot), also twist knots and simplest achiral knot. Related to 3:5 Lissajous curve.
Eq.: x(t)=(2+cos(2t))cos(3t)
y(t)=(2+cos(2t))sin(3t)
z(t)=−sin(4t)  

– Knot group representation:
(x, y |  yxy^-1xy = xyx^-1 yx)

Representation based on (RBo) lemniscate of Gerono (end connected w/ Bezier curve)

x = sint + t/10
y = sint*cost/ 2
z = sin2tsin(t/2)/4

RBo  epitrochoid –  q = 2, k = 5:

x = 3cost + 5cos3t
y = 3sint + sin3t
z = sin5t/2*sin3t + sin4t – sin6t.

RBo  Rohid Chaudhary:

x = 32cost
y =
z = 

RBo  Trochoid

w/ d/R = 6

RBo  Rohid Chaudhary:

x = cos3t
y = sin3t
z = sin2t

Squared F8k.

Practical tie of F8k.

Surface of F8k.

Geodesic line of oblate spheroid.

5^1  Pentafoil knot  

Knots | Visions in Math (wlu.edu)

– 5Fk 5^1 also known as Solomon´s seal knt. or cinquefoil knt.

– torus knot T(5, 2).    (not hyperbolic (0 hyperbolic volume))
– often named rather link than knot.

5^2  Three-twist knot  

– second and last in pair of 5 crossing knots.
– hyperbolic.
     – related to  2:3 Lissajous curve (Rpic) in its open/ doubled state w/ Phase offset 0 (1/2, 1, 3/2, 2) pi or 1/4 pi in shape cycle.
            – resp.: – nx-z-y = (3, 2, 7)
                       – phase x, y = (0.7, 0.2) – phase z is in Lassajous knot 0.            
     – twist knot- w/ 3 half twist. 

6^1 Stevedore knot  

–  6-1 Stevedore knot (Alexander–Briggs notation) can also be written as (5,−1,−1) pretzel knot.
 – hyperbolic, achiral and Twist knot- w/ four half twists.
–  Lissajous knot (Lpic) nx-y-z = (3, 2, 5)
           – Phase rate = (1.5, 0.2)

6^2 Miler institute knot  

–  6-2 knot
– also hyperbolic knot

6^3  Knot 

–  6-3 unnamed knot.
– also hyperbolic and achiral knot.

7^1  Septafoil knot  7^1

– Septafoil nother foil knot (next to 3^1 Trefoil, 4^1  figure-eight knot, 5^1 Cinquefoil + 5^2 Three-twist knot and 6^1 Stevedore knot.

9-7a:  T.  7^2

– also Twist knot

7^4 Endless knot 

– also hyperbolic knot (HW:) known also as simplest form of endless knot.
     – Lissajous knot nx-y-z = 

8^21 Knot 

– ..
     – Lissajous knot nx-y-z = (3, 4, 7)
            – Phase rate = (0.1, 0.7)

II. Knots Families and knot related groups

1. Torus knots family

– TK is always prime knot (not a composite knot/ link).
– beside unknot, no knot can be done on sphere without self-intersecting (important characteristic in topology) and hence can be drawn as simple closed curves on surface of torus (T^2).
             * simple probably in 3D (or 2Dsphere), in 2D it could be consider as crossing – self-intersection...
In Rpic is (3, 2) torus knot (trefoil) – p, q format: Red circle often mark as meridian – q– vertical and Green one b : longitude (p – horizontal) – it may be better seen on examples bellow.
– p, q is (beside orientation) same like -q, -p.  Torus (p, -q) is mirror like to (p, q). 
– p, q are in torus ≥ 2 and coprime numbers. If p, q are ?co?prime – then describe knotted curve.?

 

– knot curve – is a quartic curve (sec.Rpic) w implicit equation: (x^2 – 1) = y^2 (3 + 2y)
– standardly embedded torus is unknotted torus.
– coprime integer – relatively prime or mutually prime – if the only positive integer that is a divisor of both of them is 1: so their greatest common divisor (GCD) being 1.
8 and 9 are not prime numbers, but are coprime integers – they do not share common divisor..
Prime number is natural number (nat. nos. are 1,2… – without 0) greater than 1 that is not a product of two smaller natural numbers – see Markov chain or in r, p torus numbers.

– unknotting number of torus knot is defined: ((p – 1)(q – 1))/2.
– (p,q)-torus knot Knot group has presentation: (x,y | x^p = x^q)

(p,q)-torus knot equation:
           x(t) = (r0 + Rcos (pt)) cos (qt)
           y(t) = (r0 + Rcos (pt)) sin (qt)
           z(t) = -Rsin (pt)
– r0 – distance from center to torus inner circle.
– R – distance from center to torus outer edge circle.

 

–

‘
– Resp.:
Parametrization: x = rcos(pt)
             y = rsin(pt)
             z = -sin(qt)
                                r = cos(qt)

– or: x = (R1 + R2cosv)*cosu
         y = (R1 + R2cosv)*sinu
                                               R(u, v) – Parameterization of a Torus – GeoGebra

Torus knots examples

Noeud de billard cylindrique (mathcurve.com)
Torus solenoid (mathcurve.com) – particular Turus knots in more details.. 
– since numbers defining torus needs to be coprime and ≥ 2, than when lowest q is 2, first options are: 3, 2 – 5, 2 – 7, 2 –  9, 2 or inverted 2, 3 – 5, 2 – 2, 7 –  2, 9.
                                                                                      – q is 3, than first options are: 4, 3 – 5, 3 – 7, 3 –  9, 4 or inverted …
     – q 1 or 2 are refering as toric knots.

 

Torus knots from q2:

T(3, 2): Trefoil knot

T(5, 2): Pentafoil

T(7, 2): first heptagram

T(9, 2): first Nanogram.

Torus knots from q2 inverse:

T(2, 3): Trefoil knot (But not Figure-eight knot).

T(2, 5)

T(2, 7): first heptagram

T(2, 9): Second nanogram.

Torus knots from q3:

T(4, 3): 19th prime knot with 8 crossings

T(5, 3): 124th prime knot with 10 crossings

T(7, 3): second heptagram

T(9, 3):  third nanogram.

Q2 torus

(3, 2) Torus knot

– is obviously firs torus knot – with least possible orbits.

– Resp.:
Parametrization: x = rcos(pt)
             y = rsin(pt)
             z = -sin(qt)
                                r = cos(qt)

For T(3,2)
x = 1,25*cos(3t)cos(2t)
z = 1,25*cos(3t)sin2t

Q3 torus

(2, 3) Torus knot cheat

Figure-eight knot (mathcurve.com)
– also known Figure-eight knot – it is inverted T(2, 3) torus knot.
– as said above, torus bellow is generally not considered T(2,3), but T(3, 2) – but lets pretend the crossing in center is doubled and not a single one..

T(7, 3): second heptagram

Sine torus

2. Twist knots family

– they are easy to made (Rpic): 1) made tie in u shape (Lpic), 2) twist it from the middle in integer number times (mid pic) and 3) finally pass their ends thru top hoop (Rpic).
      – but they are harder to depict w/ some parametrization eq. – but few subgroup are exceptions, namely: figure-eight knots – 4^1, 5^2, 6^1, 7^2, 8^1 (also in left pic):
x(t) = (2 + cos (2t)) cos (3t)
y(t) = (2 + cos (2t)) sin (3t)
z(t) = sin (4t)

3. Lissajous knots and curves

– Lissajous knot (mathcurve.com)
– studied by J. A. Lissajous (1857) and N. Bowditch (1815). In 3D it get special attention by Bogle, Hearts, Jones et Stoilov in 1993.. 

– on of each particular crossing number integer is basically one knots is basically Lissajous curve: 3^1, 4^1, 5^2, 6^1 Stevedore knt
– Lissajous curves (LC) have two sin phase w/ offset and speed values for x, y 
           – phase offset of pi value is subtracted from y – so all x starting value are 0.
                                  – Lpic show shape for particular ratios values.
              – speed is obviously changing in both x and y:  Second number define number of crossing x, first number represent y crossing (in merged shape, – this number is doubled when shape is diverged). 
                                  

Lpic showing first 4 shapes w/ correct actual phase.
                    – curves do one cycle in 1pi and then going inverse (like sin wave).
First no describes crossing of all range of x axis (when shape is in close state).
           – this close shape is in 1:1 in 0, but is change w/ different ratio.
Second no describes crossing of y axis.
            – when a=b – Chebyshev polynomials – see 1:1..

 

 

 

Lissajous figure on Blackburn pendulum.

 

L pic has phase offset to depict shape change: it put 0 phase on start of cycle when shape is open-curve-like (when shape is not doubled like). 
Also rotation is adjusted to depict shapes change.
          – so f. e. second pic is 90° counter clock wise and + pi/2.

First no in ratio (q) express no of crossing y axis (red), second no (p) depict crossing y (blue).

Result of ratio is n – f. e. 1:3 – n is obviously 0,333..

 

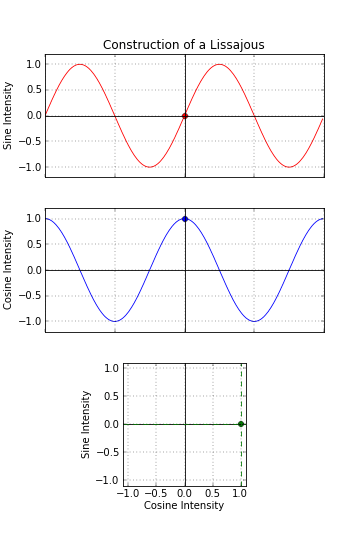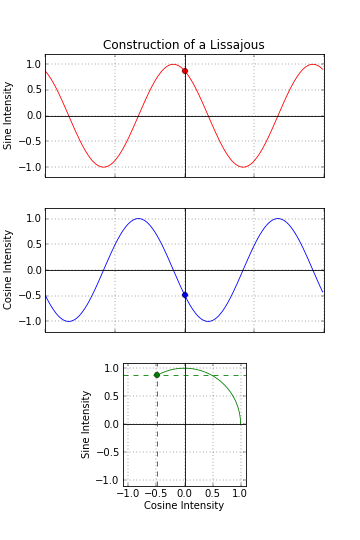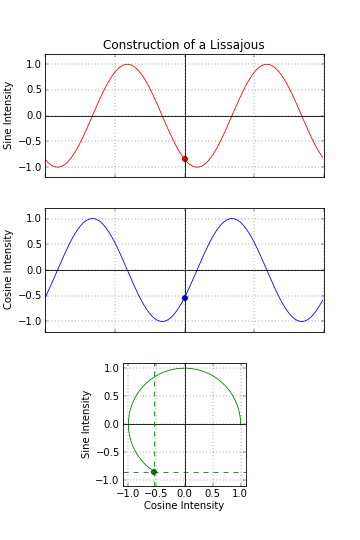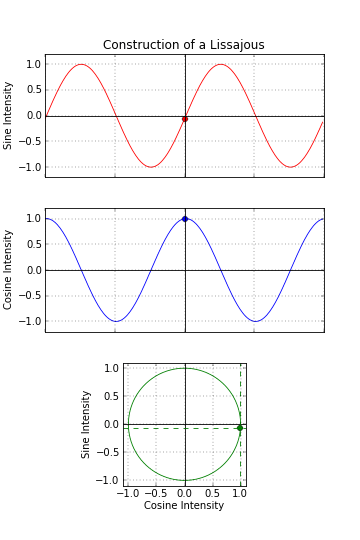
1: 1 Line – Ellipse – Circle 

Line – Ellipse – Circle – Cycle phase is same like actual phase.

– rotation is going right up (always from x = 0) expanding line to ellipse and then to circle (pics bellow).

 

               0pi

          1/4pi

1/2pi

3/4pi  

1pi  

5/4pi  

3/2pi  

7/4pi  

1:2 (0.5): Parabola  – Besace –  Lemniscate of Gerono

– 1:2 LC goes from (w/ phase 0) from Lemniscate of Gerono – Besace – Parabola. Shape cycle is 1/2 offset – starts at 1/2pi.

1:2 LC is projection on the planes passing o – passing 0z Vivani curve and so creating creating Besace.

There are in fact 2 shape cycles – 1. cycle (top line bellow): starting from open-like curve parabola, that is doubling top and squeezing bottoms thru upward leaned besace to Lemniscate of Gerono to downward leaned besace to parabola w/ ends in up direction.
Shape cycle (w/ parabola shape) starts at 1/2pi – is 1/2pi offseted.

Cycle phase:  0pi

1/4pi

1/2pi  –  0pi: Actual phase

3/4pi  –  1/4pi

1pi   –   1/2pi  

Rgif:  0z around x.

Parabola

Besace – + 1/2/ -1/2

Lemniscate of Gerono

Besace –  -1/2/ +1/2

1pi   –  1/2pi

5/4pi   –   3/4pi

3/2pi   –  1pi

7/4pi   –  5/4pi   

2pi   –   3/2pi

More on Parametric-curves (sigsaly.xf.cz) 

– Chpt. Conical roses – I. Vivani curve.
– As seen – Besace is stretched Lemniscate of Gerono, but as also even said, it is Vivani curve rotating (in uni value) around x instead of y.
      – from Vivani one can get Bifolium, Fish on curve etc..

1:3 (0,33..): 

–

2:3 (0.66..): Divergent parabola – Sextic curve
– since y is 2x crossed with merged shape – shape is mirrored and create only two figures 

𝜓 = 0 – Sextic curve when fully diverged.

𝜓 = 1/4 – Divergent parabola
– starting shape cycle

More on Parametric-curves (sigsaly.xf.cz) 

– Chpt. Conical roses – B. Transcendental spherical curves – Sinusoidal Spiral
– Divergent parabola is in Lissajous curve is special case of Divergent parabola (w/ equation: 2ay^2 = (2x + a)^2 (a – x), which is also special case of Parabolic folium and related to Tschirnhausen cubic,..

3:4 (0,75): Quartic curve – ..

𝜓 = 1/6 pi – Quartic curve.
– starting shape cycle
3 xing y;  4 x y.

– Klein’s Quartic Curve (ucr.edu)

3:5 (0,6) curves it is maybe even more obvious than on circle case, that w/ each pi curve make one circle around and so it can be in any case transformed to 3D.

–

–

4:5 (0,8) 

5:6 (0,833..) 

5:8 (0,625..) 

8:9 (0,888..) 

–

–

–

–

3. 1. 3D-Lissajous curves

Lissajous knot (mathcurve.com)
– 3D LC are actually closed Lissajous knots w/out double-point.

Standard parametrization generally

– p, q are coprime nos, r = p(q-1) + q(p-1) – 2:3 equation is:  3(2-1) + 2(3-1) = 7
            – r also define number of crosing see bellow in 2:3 LC.
φ (Phi) and 𝜓 (Psi) represent offset of the Phase for y, z. φ = Pi/2q, 𝜓 = 3/4pi.

 For n = 1 or n = m, we get a cylindrical sine wave. We get a closed curve if and only if n and m are rational.

Kartezian parametrization.

Nbased and standard parametrization examples

2: 3 LC in 3D
– 4th prime knot w/ 7 crossing (74 Knot) 
x = acos3t
y = asin2t
z = bsin7t
r = 3(2-1) + 2(3-1) = 7

Nbased writting – if n is multiple of 3:
= acos3t
= asin nt
= bsin (5n – 3)t

– if n is  odd
= asin2t
= asinnt
= bcos (3n – 2)t

– 2 cross x, 3 x y.
Starts at 1/4pi, 90° CCW (counter-clock wise). Rpic

3: 4 LC in 3D
x = acos3t
y = asin4t
z = bsin17t

–

3: 5 LC in 3D
x = acos3t
y = asin5t
z = bsin22t

–

2:3 LC in 3D:
x = acos4t
y = asin3t
z = bsin5t

Lissajous curves in polar coordinates

– Lorenz knots (LK) are also known to be modular knots (Etienne Ghys, 2006)

4. Lorenz knots

– Lorenz knots (LK) are also known to be modular knots (Etienne Ghys, 2006)

5. Ribon knots

6. Slice knots

7. Hyperbolic Knots

– hyperbolic volume of hyperbolic link is vol. link´s complement w/ resp. to hyp. metric.
– HL is 3-sphere w/ complement

4-1 Figure-eight knot.

5-2 Three-twist knot.

6-1 Stevedore knot.

6-2 Knot

6-3 Knot

7-4 Knot

1. Whitehead link

Hyperbolic knots/ links

– hyperbolic knot is a hyperbolic link with one component.
– Hyperbolic volume – Wikipedia

– hyperbolic link – Every non-split, prime, alternating link that is not a torus link is hyperbolic by a result of William Menasco.
– Hyperbolic link – Wikipedia

Borromean rings are a hyperbolic link.

8. Foil knots related  group

9. Polygram knots related  group

Polygram (mathcurve.com)

IV. Knotoids

– knotoids were induced by V. Turaev in 2012.
– knotoids are open-ended knots diagrams – they are projection of open curves, while knots are generally closed curves in 3D.

V. Knot group

– as already said above – knot is an embedding of a circle into 3-dimensional Euclidean space. The Knot group is – fundamental group of knot complement.

VI. Other knot characteristics

Seifert surface

– ..

–

–

Seifert fiber space

– is a 3-manifold together with a decomposition as a disjoint union of circles. (I also have no idea what it means)….

Real projective plane

Complex harmonic motion… 

– Complex harmonic motion – Wikipedia
–

Stereographic projection

1. Alexander polynomial

X. Chirality

– roughly about 1/4 of knots are achiral (or amphichiral): in first seven crossing these are: 4^1, 6^3, 8^3,

X. Alternating

X. Links and Alexander-Briggs notation

– 

– Alexander-Briggs notation

X. Linking, Twisting and Writhing

– linking number 

Writhe
– describe coiling of closed curve (in 3D it assume real numbers)..

Positive crossing

Negative Crossing

A Type I Reidemeister move changes the writhe by 1.
Reidemeister move – Wikipedia – more also bellow..

X. Classification of links

X. Linking number