Orbits
Parametric curves
A. Conical roses
Conical rose (mathcurve.com)
– conical rose is also – obviously – special case of rose (see at the bottom)
– conical rose is defined by number of rose bloom-leaves that are lifted – these so called liftings are also used on Helix, clelias, .. and are – as usual – marked w/ n.
– as seen bellow, particular curve can be similarly made on Sphere, or Cylinder..




– Rs are special cases of:
– hypotrochoid –
– hypocycloid –
n = 1 (1 rose lifted)
n = 2 (2 rose lifted)
n = 3 (3 rose lifted)
I. Vivani curve
Viviani’s window (mathcurve.com)
– Vivani is the conical rose with two petals – n = 2.


– it can also be (beside conical projection) a special case of Hippoed, Spherical and Cylindrical curves.

Hippoed
Hippopede of Eudoxus (mathcurve.com)
– from the Greek Hippos (horse) and pede (fetter -a greek horse fetter had this eight-like shape). Eudoxus of Cnidus (406 – 355 BC): Greek philosopher, mathematician and astronomer. Other names: horse fetter, spherical lemniscate.


Spherical
Spherical curve (mathcurve.com) and are also discussed in Spherical trig.: Trigonometric – sigsaly.xf.cz
– as mentioned Vivani curve is special case of clelia (Lpic).













Cylindrical
– Vivani curve is also special case of crown sinusoidal
Vivani is also particular case of Fish on, Bifolium and it is also Clealia w/ n = 1 (see Clelias curve bellow – in B. chapter).

–
Vivani is also particular case of besace curve rotating in extended way.. creating Lemniscate of Gerono, circle, Parabola (pic bellow).
Besace
Besace (mathcurve.com)
–

– IMO it shape between parabola and Lemniscate Gerono.
projections of the cylindric sine wave of parameter 1/2 ( Viviani’s window)

–
– curves have their basic in circle – which further evolves into: Lemniscate of Gerono
Besace – from which one can go to Vivani curve
Lemniscate of Booth
Lemniscate_of_Bernoulli
Lemniscate of Gerono
– Lemniscate of Gerono (mathcurve.com)
– x^4 – x^2 – y^2 = 0


Antihyperbolism


Newton transformation

Polyzomal curve

Watt’s curve

Devil‘s curve

In 3D sphere perspective in can be viewed as 2xwinding of sinwave around the sphere..

LB – stereographic projection

LB – stereographic projection:
– horizontal and offset.
Blue – Vivani curve.
–
–
–
–

Tear drop curves
– Tear drop curve (mathcurve.com)
– n = 1: Right Parabolic folium
– n = 2: Piriform quartic
Cartesian param.: x = acost
– y = asint(sint/2)^n

–
–
–
Lemniscate of Bernoulli
–

–
–
–
+..
II. Quatrefoil curve
Quatrefoil (mathcurve.com)
– quatrefoil res. quadrifolium is the conical rose with four petals – n = 2.

– among QC is also Clelia particularly its seam line of a tennis ball – see Spherical trig.: Trigonometric – chpt. Spherical trig.
It can be obtain: 1) Cross section point of rotating circle and line (in counter or same direction) – L1-2pic.
2) Intersection of two circles rotating around one points – L3pic.



Astroid
Astroid (mathcurve.com)
– studied by Rømer in 1674, Jean Bernoulli in 1691, Leibniz in 1715 and D’Alembert in 1748.
– named by Littrow in 1838: astroid comes from the Greek word star : astron (like the word “asteroid” designing star like objects). Other names : H4 (hypocycloid with 4 cusps), cubocycloid.

– astroid diamond shape used for Quatrefoil is special case of involutes (R1pic) or hypocycloid w/ q = 4: 4 quadrants (R2pic), or 4 cycles of rolling circle in base circle (R2pic) or w/ rolling circle having bigger r, than its rotation (R3pic).
Locus (pl. loci) – set of points (lines, curves, surfaces) satisfying particular condition(s).




– since Astroid (Lpic – blue) have 4 evoluted sides, it makes good basement for creating Quatrefoil (Lpic – red).

Maltese cross done w/ involutes in Astroid.

Double projection – using two different size circles .
Evolute – Caustic
Caustic (mathcurve.com)
– studied and named by Tschirnhausen (1681), Jacques Bernoulli (1691), La Hire (1703). From the Latin causticus, resp. the Greek kaustikos : burning.




Lpic: S is radiant
Rpic: S is at infinity


Lpic: Catenary is caustic by reflection of exponential curve y = ae^x/a.
Rpic: Evolute of catenary parametrization: x = a(t – 1/2sh2t)
y = 2acht

Principal evolute of catenary is tactrix – asymptote which is base of catenary.

Evolute of plane curve

–
–
Involute of plane curve
Involute (mathcurve.com)
– The involutes of a plane curve are the curves traced by the end of a wire tightened along and winding itself along . In other words, they are the traces on the plane of a point on a line pivoting without slipping on (therefore, they are special cases of roulettes). Thus, they also are the orthogonal trajectories of the family of the tangents to the curve, or also the curves for which the initial curve is the evolute.

Pedal curve
Pedal (mathcurve.com)
– studied by Roberval (1693), Maclaurin (1718), Steiner (1840), Terquem – named it (1847). From the Greek pous, podos : foot.
– it is homothetic image of orthomic (also have no idea what it is)).

–
Orthomic curve
Orthotomic curve (mathcurve.com)
– studied by Quételet (crc. 1822), From the Greek orthos : right and tomê : to cleave. Other name: podoid.

–
Pursuit curve
Pursuit curve (mathcurve.com)
– studied by Leonardo da Vinci and Pierre Bouguer (1732), Du Boisaymé (1811), Dunoyer (1906), and Morley (1921). Other name: dog curve.
Escape curve is linear
– simplest case.


L1pic: in red: the dog runs faster than the hare: it catches it. in green: it runs as fast: no catch possible, and in blue, even less..
L2pic: The dog has the same speed as the hare: their distance goes to a constant.

Circular escape curve
– is said to have been solved only in 1921.


L1pic: Vdog = 2 Vmaster: the dog catches up with the master.
L2pic: Vdog = Vmaster: the dog catches up with the master… at infinity.
R1pic: Vdog = 1/2 Vmaster: the distance from the dog to the master goes to and it ends up turning around a circle with radius R/2.

Base curve
Catenary curve
Catenary (mathcurve.com)
– studied by Leibniz, Jean Bernoulli and Huygens (1691). In its Latin form catenaria. Other names: funicular/sail curve.


– shape of hanging wire hanging from two points.
– it slightly shaper than parabola (Green in pic).




Lpic: Catenary is caustic by reflection of exponential curve y = ae^x/a.
Rpic: Evolute of catenary parametrization: x = a(t – 1/2sh2t)
y = 2acht

Catenary is also special case of parabolic roulette of Delaunay.

Principal evolute of catenary is tactrix – asymptote which is base of catenary.

Elastic catenary
Elastic catenary (mathcurve.com)
– studied by Delaunay (1841); Lindelöf (1861). Charles-Eugène Delaunay (1816 – 1872). Other names: elliptic, parabolic, hyperbolic catenary.




– elastic catenary is the shape taken by an elastic, homogeneous, infinitely thin, flexible wire hanging from two points (placed in a uniform gravitational field).
Delaurnay Roulette
Delaunay roulette (mathcurve.com)
– studied by Delaunay (1841); Lindelöf (1861). Charles-Eugène Delaunay (1816 – 1872). Other names: elliptic, parabolic, hyperbolic catenary.


–


Lpic: The parabolic roulette of Delaunay is none other than the catenary.

a = b = r/2^1/2

a = b = r/2*2^1/2

a = b = r/2^1/2
–
–
Cissoid

–
–
Rational circular cubic
Rational circular cubic (mathcurve.com)
– RCC are the circular cubics w/ singularity (O): crunodal, cuspidal or acnodal.
– rational circular cubics – four definitions:
1) They are exactly the cissoids of a circle and a line with respect to a point O on the circle (here, cissoid of the circle (C) passing through O with centre A(a,b) and of the line (D): with respect to O).



–
–
–
–
Orthoptic
– similarly, instead of making pedals, one can get similar 4-foils shape in astroid w/ using orthogonal (right-angled) projection:

–
Hypotrochoid
Hypotrochoid (mathcurve.com)
– From the Greek hupo (under) and trokhos (wheel): Curve created by smaller rolling circle C (black) rolling under base circle C0 (blue in Rpics).
– however line from black rolling circle can be inside or lead outside the circle (R1-2pics). If line is same length as rolling circle – hypocycloid.



3: 2 – Trefoilish figure
4: 3 – Quatrefoilish figure
5: 4 – Pentafoilish figure
7/3: 4/3 – Septafoilish fgr.
Hypocycloids
– hypocycloid is special case of hypotrochoid where drawing line of rolling circle have same length like its radius (drawing point is so actually on the rolling circle).



– 4:3 curve – Quatre curve

– w/ 3:2

Orthopolar
–
Examples of realistic quatrefoil





R = a*(sin2t)^1/2
R = a*(sin2t + (sin6t/4))
R = a*(sin2t) + (sin^2 4t/4)
R = a*(sin2t)^1/2
R = a*(sin2t)^1/2
1:3
–
Conchoids
Conchoid (mathcurve.com)
– conchoid are special type epi/hypo-trochoid – drawing line has drawing points on both sides and whole line is drifting sideways.

–

Centered trochoid
Centred trochoid (mathcurve.com)
– centred trochoid are special type epi/hypo-trochoids resp. conchoids – drawing point is not on the end but in the middle of the line. So it is not epi (over), nor hypo (above), but centered (in between).
–



1:3
Polytrochoids

–
–
Trisectrix and ceva
Trisectrix
Sectrix curve (mathcurve.com)
-is special type of curve.,.

–

Ceva
– (2n+1)-sectrix, and is called “Ceva sectrix”.

5-sectrix of Ceva
–
Cyclic harmonic curves

– studied by R. E. Moritz (1917).
Other names: geometric petal, botanical curve, Trojan rose (in the case e > 1), conchoid of a rose, circular sinusoid, Moritz curve.



–
Cassini curves
Cassinian curve (mathcurve.com)
– studied by Serret (1843), Dominique Cassini (1748-1845). Other names: isodynamic line, lemniscate.

– w/ n = 2 – Cassini ovals
– n = 2, q2 = -q1 – pencil of circles.
– b < a –
b = a – sinusoidal spiral
b > a – simple closed curve



n = 3
n = 4
n = 5

–
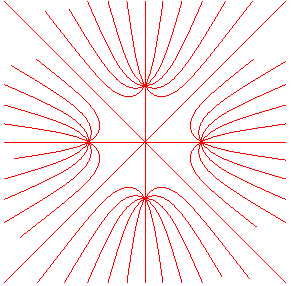
Pencil of circle
– is shape get w/ magnetic (resp. electrostatic) fields: Orthogonal trajectories (mathcurve.com)
– is special case of Circle curves – Circle (mathcurve.com)

– red lines are initial curves, blue lines are orthogonal curves.
–
Stelloide
Stelloide (mathcurve.com)
– Cassini curves and Stelloids are reciprocal images of coordinates lines.
–

Circles
Circle (mathcurve.com)
– above are mentioned pencil of circles, but they..
III. Trifolium
Trifolium (mathcurve.com)
– trifolium is the conical rose with three petals – n = 3.
– trifolium (Latin): trefoil. Studied by G. de Longchamps (1887) and Brocard (1891).



Deltoid
Deltoid (mathcurve.com)
studied by Euler (1745) and Steiner (1856). Delta: Greek letter reminder of the shape of the curve. Other names: three-cusped hypocycloid, H3, Steiner hypocycloid, or tricuspid curve.

– deltoid triangle shape used for Tre-foil is special case of involutes (R1pic) or 3 cycles of epicycloid rolling circle in base circle (R2pic) or w/ rolling of epitrochoid – w/ bigger r, than rolling circle (R3pic).





XX

XX
– similarly like w/ Beetle curve..

XX
– projections from a cylindric sine wave with 3 arches, through a 3D basin.
– also special case of n = 3/2 Hypotrochoid:

W/ q = 3 and w2/ w1 = 2.
XX
XX
–
Beyond Conical curves..
–
Bifolium
XX
– parabola..


Epitrochoid
Epitrochoid (mathcurve.com)
– From the Greek epi (over) and trokhos (wheel).

–
– similarly to hypotrochoids, if the length of drawing line in rolling circle is same like its radius, it is epicycloid.
Limacon
Limaçon of Pascal (mathcurve.com)
– studied by Dürer (Arachnes) in 1525, Etienne Pascal in 1630, and Roberval (who named the curve) in 1650. Also known as limaçon of Pascal or Pascal’s Snail.

– special case of rose n = 1 – so also special case of epitrochoid (Lpic) – w/ rolling and base circle same size and drawing line in length of a.
– also pedals of circles (Rpic – see their green envelopes circles bellow)





– evolutes of limacon are also caustic reflection of circles.
The curves with equation (cissoids of a circle passing by O and a rose) provide an elegant filing of the limaçon; here, k = 55/37 (idea of Thierry LEGAY) .




Durer folium
Dürer folium (mathcurve.com)
– studied by Albrecht Dürer (1471 – 1528): German painter and engraver.

– special case of rose n = 1/2 – so also epitrochoid w/ q = 2 and k = 3 (w/ drawing line 3x of r of rollig circle that is 2x smaller).

Mating profile
Gears (mathcurve.com)
– studied by Euler and by Miquel in 1838. Other name: syntrepent curves (given by Miquel)



n = 1






n = 2
n = 3
n = 1/2


cardioid and mouth.
–
Helices (Helix)
Helix (mathcurve.com)
– are define by surface on which they are rolled.
–
–
Cylindrical helix
Circular helix (mathcurve.com)
– first study (that did not reach our times) credited to Apollonius of Perga (2nd century BC) and second study by Geminus of Rhodes (1st century BC). Other name: circular helix.



Conical helix
Conical helix (mathcurve.com)
– Curve studied by Terquem in 1845. Other name: concho-spiral.


–
Elliptic helix
Elliptic helix (mathcurve.com)
– studied by Dürer (Arachnes) in 1525, Etienne Pascal in 1630, and Roberval (who named the curve) in 1650.
– also known as limaçon of Pascal or Pascal’s Snail –


Elliptic cylinder

Copula – 8 elliptical cylinders.
Chebyschev
– chebyshev is in its simplest form in the Bitwig´s Grid.
– similar to Lissajous curve with a = 1 and b = nat. number (than its Chebyshev polynomials of the first kind of degree N – Chebyshev polynomials – Wikipedia
B. Transcendental spherical curves
Clelias
Clelia (mathcurve.com)
Curve studied by Pappus and mainly by Guido Grandi (1728), who named it clelia (after the countess Clelia Borromeo).
– Clelia is also limit case of torus selenoids (L1-2pics).




– system again based on n, w/ p and q.

generalized Plücker conoid :



Seam line for tennis ball
– is limit case for Clelia n = 2 and it is also intersection between Plucker conoid and sphere.






n = 1
n = 2
n = 3
n = 4
–
–

–
Sinusoidal Spiral
Sinusoidal spiral (mathcurve.com)
– studied by Maclaurin in 1718. Name given by Haton de la Goupillère in 1857.
– special case of: Conical Roses and should be compared with them..
– Cassini curves
– Stelloids
– while they are by it nature transcendental, they can be express in algebraic geometry by polar equation:
Algebraic: r^n = a^n cos(nt) (only if n is rational (just not 0)) Polar: ρ^n = a^n cos(nt) (n – real number)
– w/ opposite rotation sin can be also used.
– obviously polar eq. are not easy to transform to cartesian, but they (as here) often easier to write than its cartesian counterpart.
Rectangular hyperbola (n = −2) Lemniscate of Bernoulli (n = 2)
Line (n = −1) Circle (n = 1)
Parabola (n = −1/2) Cardioid (n = 1/2)
Tschirnhausen cubic (n = −1/3) Cayley’s sextet (n = 1/3)

Positive n

Negative n


Divergent parabola
Divergent parabola (mathcurve.com)
– studied by Newton 1701.
?Any cubic is projectively equivalent to (i.e. is the image by a real homographic transformation of) a divergent parabola – Newton theorem.?
Cartesian equation: where P is a polynomial of degree 3 (Cubic): crunodal , acnodal, cuspidal ..
– DP is also special case of parabolic folium..
red: elliptic cubic with an oval – Elliptic cubic (mathcurve.com)
green: acnodal cubic
blue: elliptic cubic with a branch
yellow: crunodal cubic
magenta: cuspidal cubic

This divergent parabola is 2:3 Lissajous curve w/ 𝜓 = 1/4 – equation:
2ay^2 = (2x + a)^2 (a – x)

Tschirnhausen cubic
Tschirnhausen cubic (mathcurve.com)
– studied by Tschirnhaus (1690), L’Hospital (1696) and Catalan (1832). Named 1900 – R C Archibald, adding “en” at the end of Tschirnhaus’ name. Other names: Catalan trisectrix, L’Hospital cubic, orthogenid. Ehrenfried von Tschirnhaus (1651-1708): German geometrician and physicist.

Butterfly curve
– transcendental plane curve discovered by Temple H. Fay (1989 – US university).

– parametric eq.: x = sint(e^cost – 2cos4t – sin^5(t/12))
y = cost(e^cost – 2cos4t – sin^5(t/12))
– polar eq.: e^sint – 2cos4t + sin^5(2t – pi/ 24)

Ribacour curve
Ribaucour curve (mathcurve.com)
– problem posed by Jean Bernoulli (1716), solved by Taylor (1717). Studied by Ossian Bonnet in 1844 and Ribaucour in 1880.

k = 0 – point. w/ n = -1 – line.
k = 1/2, n = -2 – rectangular Sturm roulette or right lintearia.
k = 1, n = inf. – circle.
k = 3/2, n = 2, – lemniscate of Bernoulli.
k = 2, n = -2 – cycloid with cuspidal points on (D).
k = 3, n = 1/2 – cardioid.
k = -2, n = -1/3 – parabola.
k = -1, n = -1/2 – catenary.
k = -1/2, n = -2/3 –
Positive k


Case k = -1/4, -1/2, -1 (catenary), -2 (parabola).
Rhumb lines
Spherical helices
Spherical cycloids










L1-2: Narrow cone on conical bowl 1: bulged down, 2 – bulged up,
R1-2: Wide cone on bulged down bowl, 2 – narrow cone pulsed w/ wider cimbal hat.


Spherical trochoids



Satelite curves
Curves of spherical pendulum
Rose
Rose (mathcurve.com)
– 1looks: Guido Grandi 1723 & E. W. Hyde 1875. Names: rhodonea, Grandi rose, multifolium.
Polar eq: ρ = acos(nθ)
Area of petal: (π/4n)*a^2
– Rs are special cases of:
– hypotrochoid –
– hypocycloid –








